Visual Patterns

Have you seen this excellent website? It was like nondenominational math teacher Christmas when I happened upon it!

I definitely blogged last year about the Rectangle Pattern Task, which I’m in love with. I love the mix of linear and quadratic patterns, and the low floor high ceiling aspects. So great! This website has over 200 similar things, aka I do not have to create my own. I emailed Fawn Nguyen who created the site just to say THANKS, and she emailed me right back with the answer key. I did not think I would need it, because I’m super conceited when it comes to my own high school math knowledge, but a couple of those threw me for a loop. I was actually having a ton of trouble with the third one!

This year I decided to use that Rectangle Pattern Task as a springboard into differentiating between linear and quadratic growth. We took some notes which you can kind of see in the background of the next picture, behind some of the visual patterns:

We’re going to do linear modeling as the very next topic, plus we do a ton with quadratic factoring and quadratic modeling later on, so it was really important for them to know what the graphs look like, what the growth is like, and what the equations are like. I’m glad we’re starting with this because we’ll keep referring back to this.

Today I had them in pairs sorting the patterns into a pile for linear, a pile for quadratic, and a pile for neither (the “neither” was a fractal, which is exponential growth). Then they wrote the equations for the linear ones. I was going to start having them write the equations for the quadratic ones, but it was too many objectives for one day. We’ll get to that later when it actually makes sense. Although honestly the linear ones have a clear procedure that always works, and the quadratic ones do not, at least not one which is obvious to me. I’ll keep puzzling with it.

I’m going to see how things go on the assessment, but I felt like I was seeing some breakthroughs. And if they aren’t ready for the assessment, I can give them like 200 practice problems. YAY.

Intro to Math: Circles and Squares

School is back in session! One of the students I tutor apparently has no homework tonight, otherwise I don’t know when I would have had time to put this into writing – things got busy in a hurry.

I’m doing the whole #teach180 thing so if you’re desperate to see more frequent updates from the classroom you can follow me on Instagram, @multiplefactorsi. I’ll be posting every day, held accountable by a reminder on my phone. I hate tiny little red numbers on that screen, so you know I’ll be following the rules.

Anyway! The first week of math class I always do “intro to math.” We started with some talk about what topics in math we were going to do over the year, and then we spent some time on an arts integration project inspired by these tasks for small children. This would have been awesome if we had more time, or maybe they would have gotten old – who can say? A couple students finished them beautifully at home, and others have kept their unfinished projects in case of momentary boredom. I’ll attach that whole assignment.

PDF of the assignment: day-1-arts

The second day was all about seeing things from multiple perspectives and integrating multiple viewpoints into collaborative work. We started with a number talk, something I loved when I first saw it but just never used. I took the one from YouCubed’s “Week of Inspirational Math,” week 2 day 1. I had been very nervous that our conversation would be nothing like the thought-provoking and joyful example video, but this went amazingly. Here’s our board:

Inspired by Sarah at Math = Love, who was in turn inspired by other bloggers, we then launched Broken Circles. That was great! I love hearing students talk about math, but I also loved the no talking rule. It’s also an inspired touch that one circle completes itself. In one group, the person with the “A” pieces sat there, self-satisfied while the rest of the group struggled, and it was kind of glorious. It’s almost like the point of this task was to show that working together and paying attention is crucial.

Between that and our next collaborative task, we went over our group norms. I translated them into Spanish for an extra touch, and perhaps that will inspire me to do more group work in Spanish class? Time will tell.

The end of Wednesday we started the Pentomino task – I blogged about Pentominoes last time I did it, SO long ago! This year I didn’t leave as much time and consequently they didn’t come up with quite as many combinations, but I do still think it was a useful exercise in visualization and pattern recognition. I’m kind of in love with my independent reflection for that task, attached. Why indeed can you not build a 6×6 square?

Independent Reflection PDF: pentomino-ir

Things are shaping up, but I already know I won’t have nearly enough time to blog as I’d like : 0

Factoring Amazing Race

Sometimes I have a strong temptation to use my blog solely for successes and never mention anything that isn’t great within my classroom. But I recently had a realization so simple that I don’t know how my teaching could possibly have been effective before it! Realization: students won’t work together effectively until they are together on a team.

We had this excellent all-school camping trip last week, but as a consequence class did not take place for an entire week. I was concerned that they would have forgotten everything, so for my Math 2 class I created an Amazing Race game to review and practice binomial factoring. All along I had been encouraging them to work together and ask each other questions, but everyone was either lost and totally un-focused, or focused on doing their own work, not motivated to help others.

I had them in 3 groups for the Amazing Race. I put three students who were on the verge of full understanding with an extremely competent but extremely quiet student. My thinking was that the quiet student could shine and the on-the-verge students would quietly listen in order to gain full understanding. This group was fairly effective although never fully cohesive – I mainly saw them interacting one-one-one rather than as a full group. I put four on-the-verge but potentially less-motivated students together so that they would all have to participate fully in order to understand. This went well – some of the best conversations came out of this group. Then I put a brilliant and patient student with a very silly but very smart student and two students on the struggle bus. I think that at least one of the strugglers is doing really well after that, but the other one is still struggling. I’m feeling sad about this but I’ll catch up with her on Make Up Work Day.

Launch – Explore – Discuss

Happy Saturday, blogosphere! I’m currently located at school, about to do my second round of ACT/SAT prep of the day, and furthermore drink my third cup of coffee of the day. In between, my colleagues and I were tabling at a conference for twice-exceptional students. Tabling typically involves me excitedly explaining our school to anyone willing to listen, and ramping up imaginary rivalries with our fellow small schools. I did try to tone that down this time, though, because I suddenly want to do some classroom observations (aka spying) at other small schools.

The congregation of the church we rent our space to is slowly arriving, and that is the only thing weirder than being at school by myself. There are also two cats in the office building instead of just one like usual,

None of this is what I had intended to discuss! I have been implementing and blogging about collaborative learning for years, explaining that we had learned all of these techniques and ideas in college and I had wanted to try it. All this time I had been ignoring what I have recently discovered is an important element: the discussion. What you’re supposed to do is launch the task by explaining the directions and process, have the kids explore the material on their own, and then have a discussion as a full class to bring together their ideas. Since I was so focused on having the kids prove to me and themselves that they knew the material as an individual, I’ve been skipping the last step.

Such a poor choice! Wednesday we spend most of class on a discussion of the Rectangle Pattern Task I discovered last year. I love this task so very much. It’s the physical embodiment of “look for and make use of structure.” As I had learned to do in college, I structured the discussion around which groups had discovered what in a nicely-phrased way, making sure that everyone would have a chance to speak. Here are my notes:

The groups shared the patterns they had recognized. They predicted step 0 as just 2 blue squares, then determined that each time you add 4. To find the pattern, I wrote that out like this:

This made it easier for them to see that the nth iteration would have 2 + 4n blue squares. Love it!

To discover the green and red patterns, which are quadratic, we went more visually. That’s the squares you can make out in my notebook. The students described that the pattern of green squares is that on each side, you add another row, and that row will include 2 more than the previous. I drew this out as they described it:

Then I asked them to find the largest square in the first one. They said 1. I asked for the largest square in the second. They said 4 at first, then clarified that that was 2 by 2. For the last one, someone pointed out that there are many different 2 by 2 squares in there, which is true. I asked them if they could re-arrange the boxes to create a larger square than that (should I have waited to pose this?). One poetically described that process as “you take the wings off of the bird, and you put them on the bottom.” I illustrated it slightly differently, and then gave everyone paper to cut in order to create squares. This was the end result here:

The pattern for one side is then n squared plus n!

The next day the room was entirely silent and productive as brilliant math learners completed their independent reflections and then determined the patterns on yet another set of box designs. Next week we’ll discuss those, then I want to give them an assessment on this [which I have yet to write], and then we’ll work on factoring in a hopefully visual / non-terrible way.

Group Norms

Working collaboratively is an incredibly important skill, and increasingly so. So in addition to teaching math, I’ve been working on strategies for teaching communication and collaboration skills.

I got a jump on this during bonding week this year. Every year we divide the school into small groups of maybe 5 or 6 and task them with creating boats. We have this rotation – year 1 these boats are strictly cardboard and duct tape, year 2 strictly trash bags and duct tape, and year 3 cardboard, trash bags, and duct tape. It’s year 3 but this picture is from last year:

Chaos, right? But super fun chaos, and we get more buy-in than you’d expect. Even still, we had noticed this tendency for boat group communication to be subpar. The groups would usually defer to the ideas of whoever was loudest, kids sometimes got mad that their idea didn’t feel listened to, and without a teacher consistently in the room (which would ruin it in other ways), it was totally OK to not participate for kids who didn’t feel like it.

So this year we had them do limited-resource challenges in small groups, and then reflect on these group dynamics upon entering their boat groups. We orchestrated the groups so that nobody was in a group with someone they just worked with, so they could talk openly about their experience. I wrote up a set of reflection questions:

Communication Discussion Questions:
1. What was the most challenging part of communicating with your previous group?
2. Did you feel that your ideas were listened to?
3. Did you always feel comfortable sharing your ideas?
4. Did you feel that you listened to other ideas? Why/ why not?
5. What qualities in someone else make them easy to communicate/collaborate with?
6. What qualities in someone else make them difficult to communicate/collaborate with?
7. Do you find it helpful when someone steps up to be the leader, or does that make you more reluctant to share?
8. What can you do as a group member to make sure nobody is dominating the discussion?
9. What can you do as a group member to make sure quieter people are joining in?
10. What can you do as a group member to make the decision-making process easier?

So now in my math 2 class we’ve started our first group task, the rectangle pattern task I discovered last year. Before breaking into groups we went over the group norms, based on concepts we talked about in my college classes and the book Designing Groupwork by Elizabeth Cohen. Group norms:

For a productive group…
1) Stay in your group
2) Ask the other group members first
3) Everyone is accountable for what the group is doing
4) You are responsible to ask for and offer help

I like the last one best although the first one is a close second.

Best question ever: “wait – are we doing this to practice working in groups or to learn the math?” Answer – both!!! I think I exclaimed that with three exclamation points in class as well.

Tomorrow we finish the task in math 2 and launch the vector fields task in math 4.

Intro to Math Week Year 3: Arts Integration Edition

Just finished my last academic day of the first academic week of the school year. As it has been for the last couple of years, this week is “intro to math week,” and this year I focused specifically on arts integration, keeping the mathematical standards of practice front and center.

On day 1 we spent some time on the syllabus, focusing on class procedures and previewing the upcoming units. Thanks to keeping this blog I have plenty of pictures of previous classes doing the work they’ll be doing, so it’s not just a line about functions or data or whatnot on a sheet of paper. Then I had them each take a Math Attitude Survey. Somewhat unsurprisingly, most of the new ones had some pretty negative associations with math. Kids also weirdly LOVE sharing bad experiences in math classrooms, so it’s a nice first day icebreaker. I took everyone’s three words and put them into a word cloud:

I’ve always been too scared to re-administer the survey at the end of the year, but I think I should do it, or at least have them give me three words again.

The next day was all about arts integration. I had them re-examine the mathematical practices and compare them to the National Core Arts Standards, since I had personally noticed so many great links. Some of them were a little unsure at first, or had trouble understanding what individual standards meant, but they didn’t shy away from asking each other or me for clarification, and the resulting conversations were pretty cool.

Then we watched this TED talk by Daina Taimina, or at least most of it – it’s super long [for my kids’ attention spans & non-university math levels] and the important parts are at the beginning and end. I love this talk so much though. It inspires me to see her construct her own understanding, especially given her initial troubles with the subject, I enjoy seeing stereotypes smashed, and is the perfect example of arts integration. The art form makes the mathematics more concrete and comprehensible, and the mathematics provides structure and context for some interesting-looking pieces.

Typically I have some major emphasis on group norms, but I didn’t want to insert something else random into this week, so instead today we just had an extended journal reflection and then dove right into our first topics. I’ll teach them the group norms as we start doing our first group tasks. I realized earlier that I’ve never actually blogged the group norms, so I’m working on a separate post about that.

So far things are going well BUT hey it’s only the first week.

“Learn What You Missed Week” and MI stations

Greetings! I have recently returned from this year’s senior trip. As you can see from my wrist accessories, we went to the Rock and Roll Hall of Fame in Cleveland and the Franklin Institute in Philadelphia.

We can worry about how cool my tattoo is later. Anyway, before the trip happened we were back in class for 2 days after exams. I will be honest and say that I was not extremely in favor of this decision – I did not feel like I could come up with 2 days worth of engaging lessons on “going over the test.” Ick. Instead of trying to fix every mistake they made on the test and magically make them understand what they hadn’t just one week prior, I created an initially simple-seeming activity.

For each of my classes I identified the three most-missed objectives. In case you are curious, for math 4 they were modular arithmetic, fractals, and summation notation (sigma). For math 3 they were complex number operations, data, and exponential growth and decay. Finally, for math 2 they were factoring, similar figures, and probability. Then for each of the 3 objectives I found or created (usually created) a task for each of the 9 intelligences in Gardner’s theory. Those are: interpersonal, intrapersonal, existential, naturalistic, logical/mathematical, visual/spatial, verbal/linguistic, musical, and kinesthetic.

So that’s 3 classes x 3 objectives x 9 intelligences = 81 tasks. Luckily the art objective for exponential growth also worked for fractals so actually just 80 but still! Luckily again, these went really well, and it was all worth it.

This was the kinesthetic data task, where they had to throw the paper glob a bunch of times and record the distance, then find the mean, median, etc. I like the looks of that full page of mathematical text – that is not the work of an un-engaged math learner. This also shows the bin of algebra tiles, which I’ve never seriously used but actually really like. I experimented with them for the kinesthetic factoring task, and I think they have potential.

I printed the tasks on colored paper and cut them out so that they could just select one and then grab it and do it. Can you slightly see that the big one has music notes on it? I think that particular music task was one of the ones that was a bit of a stretch actually – they had to look at the notes and graph the melody on a complex plane, which probably doesn’t have musical meaning. The best ever musical task was the musical data one. I drew inspiration from this & had them record data about their favorite songs’ danceability, valence, and speechiness.

There’s a lot going on in this picture. The picture of ghosts was for a task inspired by this which is very neat. The reason why it is ghosts is probably because of the manipulatives I created to practice multiplying complex numbers. Those are in the blue cup in the front of the picture. They are pretty much algebra tiles, only instead of “x” blocks there are positive and negative ghosts to represent i. The positive ghosts are smiling and the negative ones are frowning. It was cute, initially confusing, and potentially very effective.

I’m done teaching until the fall but I think I will still have plenty of things to write about. We shall see.

Group Exams and Assessment in General

Exams are over! As a teacher, I secretly love exams – I love grading in brightly-colored pens, noticing trends in student performance, and somewhat shamefully, I enjoy a few days of just sitting. It is a really interesting balance, though, of stressing the importance of demonstrating knowledge on a culminating assessment without heightening any students’ anxieties. All last week and now this week I’ve been on the verge of sending mixed messages, applauding students for doing well but reassuring ones who didn’t knock it out of the park that their grade won’t drop down catastrophically.

The rest of the year I give short, low-pressure assessments as soon as students feel they’ve mastered a particular objective. I think that making these as small a deal as possible helps get more accurate data – students aren’t nervous about their performance, they’re just demonstrating their knowledge.

I tried to make the exam pretty non-threatening as well, even though it inherently feels high-pressure. A big part of that is the group exam. This is usually a multi-part task with multiple entry points to maximize student participation. This year for math 4 I had them build three iterations of the Koch snowflake out of craft sticks. I was going to have them build 4 but we would NOT have had time, or probably space. Then they had to find the area of each iteration based on the patterns of exponentially-increasing triangles. It turned out very nice!

My favorite part about this was that they walked in for the exam to see all the tables pushed to the walls and just knew something was up. I’ll attach the text of the group exam as well: Math 4 Group Final 2015

I should note that I do a group final as well as a standard individual final because of the way exams are scheduled at my school – I have each class for 1.5 hours before lunch, then another 1.5 hours after lunch. I didn’t think that it would benefit anyone to write a 3-hour math test. These tasks could work in a non-assessment situation, too, though.

For math 2, we’ve been doing all this great work with polyhedra so I had them continue for the group exam. As a sidenote I’ve been very inspired by this myself and have been hard at work crocheting pentagons for a dodecahedron – I hope to post that at some point. This exam was centered around the tetrahemihexahedron, which I think is amazing. I had them cut out nets and fold them with basically zero guidance – they did an amazing job intuiting how these should be folded. Then I asked them to create toothpick-and-marshmallow structures with things in common with this concave shape, such as the cuboctahedron below with the same vertex figure, 2 squares and 2 triangles:

That’s actually one I made, theirs was kinda lopsided, but they tried SO HARD. Most of the time my philosophy is that trying hard is NOT the same as doing good work, but sometimes I let lopsided polyhedra and the like slide.

Here’s the full text of the task: MATH 2 GROUP EXAM final 2015

So I’m almost done in the classroom, but I still have enough odds and ends to be posting well into the summer. I’m actually about to head back to school now to see the seniors present their projects, which is always a really nice culmination of some interesting independent student work. Plus I made cookies!

3D Figures

I remember in college we had this super big “unit plan” project where we had to write out lesson plans for every day of a unit about a particular topic. Some classmates felt this was unrealistic because nobody would create an entire unit from scratch. I hoped that it was unrealistic because I wanted to create all of my units from scratch, which I kind of am now, and I didn’t really think it was possible to devote all of this attention to every detail of everything. Our professors gave us some really good advice, that if you focus on making one unit each year really good, then you can save that, and the next year you can focus on making another one really good, and then eventually you can teach everything to the best of your abilities.

This is not to say that I have created a really good 3D figures unit, just that I’ve been improving it steadily. I had planned on revamping the similar figures stuff, but I ended up only slightly tweaking that. 3D figures definitely have so much potential.

I have 2 sections of this class, and each is focusing on something slightly different: one on the visual aspects, and one on the algebraic aspects. This is giving me a great chance to experiment. I have this exciting exploration with marshmallows and toothpicks that I’ve had kids do in the past. It’s designed to have them discover the Euler Characteristic, V – E + F = 2, for vertices, edges, and faces.

Cool Platonic solids, right? I had to look this up, but Platonic solids are polyhedra with regular shapes as faces. Because of reasons I’m having them investigate next week while I’m at the NCTM conference, there are only 5 of these. Making an icosahedron out of toothpicks and marshmallows is extremely difficult, FYI.

We’ve also been working on volume and surface area. We found the volume of this little house in our school’s back yard by measuring everything and splitting it into a rectangular prism and a triangular prism.

When I was looking for non-terrible proof stuff I came across this and needed us to do it.

See, the surface area of a sphere is 4 times the area of the great circle! I love this so much. We proved the surface area of a cone using party hats and sector area – some great review, and great fashion statements! This is going to allow us to compare the surface area of a cylindrical cup and a conical cup with the same volume.

There are so many more things we can cover in the 2 weeks (!!!) that I have left for content this year. Stay tuned for another post!

Since November

Haven’t blogged since November? Oops. In my defense, a great deal of the time between now and then was just winter break, exam review, and then exams. I’m also basically teaching the same things as last year – in Math 4 they just finished up the Math Words Task and are moving on to the Fractals Task, and in Math 3 we just finished up our discussion on Zero and asymptotes. In terms of new things, here are four exciting moments in math:

IM 3 Infinite Series Argument

Before just telling them the formula for an infinite sum, I wanted the kids to really understand what infinite series really mean. We all went outside and chose a little tree. I walked halfway to the tree, then half that distance, then half that distance. I regret not having them walk halfway themselves, but I was cold and wanted to go back inside quickly. Next year I will be a better teacher. I asked, “will I ever get to the tree?” Consensus? Basically.

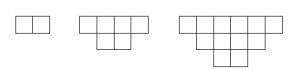
Before our whole-class discussion I had given them the pie graph to color in and asked them to make a prediction, basically the exact same situation as the tree only with 1/3 in there instead of all 1/2’s. Most of them said “it looks like it’s going to be 3/4 because you keep adding smaller and smaller pieces.” At least two of them simply couldn’t accept that infinite pieces added to a finite area. This led to an excellent debate and demonstrated a clear need for the a/ 1-r formula.

IM 2 Probability and Combinations

If I’m honest, I am not a big fan of probability. It doesn’t always make sense to me, there are lots and lots of formulas, and it never really rings true to me. In an attempt to make my probability unit feel a little less contrived, I took a picture of all of my gym socks. They just felt like a probability word problem to me. I asked the kids to, among other things, tell me the probability that I reach into my sock drawer and get a matching pair, and it’s super unlikely. I also received plenty of unsolicited advice about keeping sock pairs together.

When we got to the combinations part, it was even easier to keep things real-world. I taped some stations around the tables asking about potential boxes of cupcakes or rice bowls at ShopHouse. Have you been there, BTW? It’s Vietnamese/Thai Chipotle and it’s delicious! There are 2,304 different combinations to choose from and 192 are vegan!

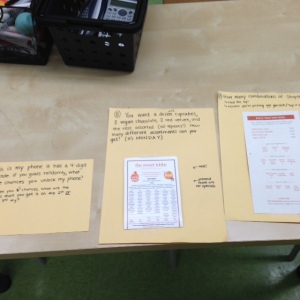
It’s disappointingly difficult to read these but the right one is the ShopHouse menu, the middle one is about getting a dozen assorted cupcakes at The Sweet Lobby (they won cupcake wars!), and the left one asks them for the probability that they can unlock my phone in the 5 tries you get. The probability is 1/2000 so I didn’t feel too nervous leaving my phone out.

This definitely felt real-world. One of the kids almost refused to do the cupcake problem because a dozen seemed too expensive. Two of them saw the ShopHouse menu and were like “OK, I want brown rice, chicken, red curry…” before I asked them to read what the problem was asking. Students in other classes did the problems just because they were curious, which I obviously liked.

To get students to do practice problems like they sometimes just need to do, never underestimate the excitement that some tape and colored paper provides. The math of counting menu items from an actual menu is not different from the math of a worksheet that says “at Todd’s sandwich shop, there are 5 types of bread, 3 types of cheese, and 8 types of meat…” BUT the investment level certainly is.

On the test, I actually wrote a really similar problem to my un-exciting example just there, only the sandwich shop was called Jenny’s Sandwich Jubilee and you could potentially choose a banana bread cottage cheese pastrami sandwich! RIP Mitch Hedberg.

Speaking of Jubilees …
The word “jubilee” is really having a moment in my classroom. Did you know that the word “Jubilee” is a Biblical-times word for a period of debt-forgiveness? Thanks NPR! Evidently they had a jubilee in Iceland for mortgages, and we listened to the story to compare mortgages there with the mortgage formula we learned for US mortgages.

Then we did a search-and-rescue that spelled out JUBILEE. Meanwhile in math 2 I not only named the fictional sandwich shop Jenny’s Sandwich Jubilee, I also asked them to compare potential re-arrangements of JUBILEE, HOLIDAY, and REVELRY.

This was a lot. I should just blog more.